Rendezvous Involving Change of Course and Speed

At 1100 hours, ship X with an injured crew on board is bearing 305° T, 48 nm from survey ship Y, which has a doctor on board. The survey vessel is presently steering 240° T at 9 knots. After 1 hour, the survey ship will alter her course to 000° T and increase speed to 12 knots and then maintain it throughout. Find the course to steer by ship X in order to rendezvous as soon as possible with the other ship if the maximum speed is 15 knots. Determine the exact time of the rendezvous.

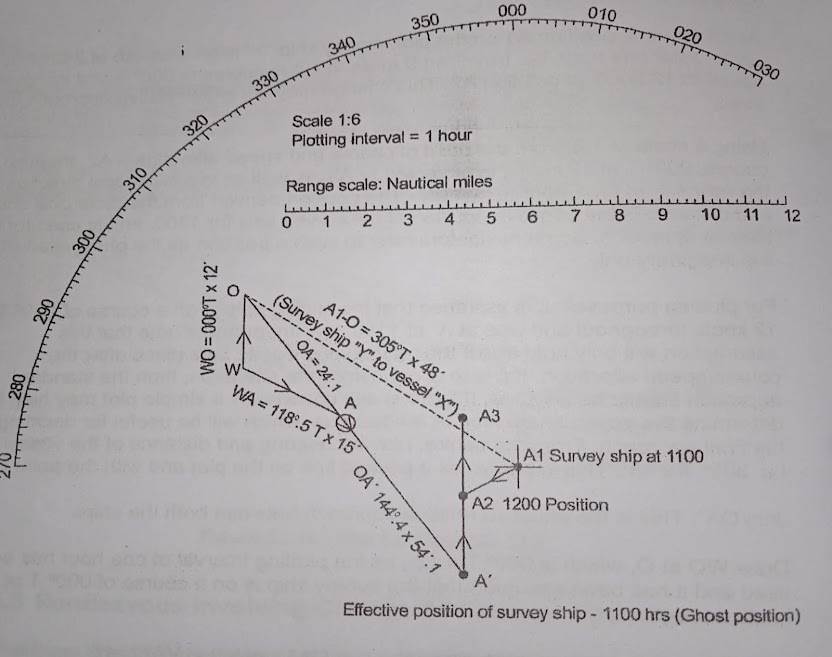
Rendezvous Involving Change of Course and Speed

Around 1100, survey ship Y is in position A1 with a course of 240° T and 9 knots. At position A2, it changes direction to 000° T and speeds up to 12 knots after an hour.

The new course, 000° T at 12 knots, is projected from that point of course and speed alteration (A2), as well as in a reciprocal direction at the new speed for 1 hour to point A’.

The position derived from the reciprocal course and distance is the effective position of the survey ship for 1100 hour and is used for the relative approach. It’s known as the “ghost position”.

For plotting purposes, it is assumed that the survey ship was at A’ at 1100 and is currently on a course of 000° T at 12 knots.

Plot the bearing and distance of the other ship X (305° Tx 48′) from the center.

Join OA’. This is how the two ships should approach one another. Due to the hourly plotting interval and the assumption that the survey ship is continuously traveling at a speed of 12 knots while on a course of 000° T, draw WO at O, which is 000° Tx 12′.

Mark A along the line OA’ with the origin W so that WA is 15 since the maximum speed of vessel X is 15 knots. The course that vessel X must follow to reach their rendezvous as soon as possible is indicated by WA. The figure shows WA to be 118°.5 T.

Time of rendezvous = 1100 + [(OA’ / OA) x plotting interval]

1100 + [(54.1 +24.1) x 1]= 1100 + 2h 15m = 1315 hrs.