Parallel Sailing
- Departure and Arrival positions are on the same latitude. This is called parallel sailing.
- In parallel Sailing, dep is the distance.
- Departure = dlong * cos latitude
- Assume that the earth is a perfect sphere.
Find the distance travelled by a ship on a course of 090° T at latitude 45° N. If its longitude changed by 20°. If latitude was 60° N, find the distance.
20° = 20 * 60 = 1200′ of arc
For 45° N:
dep = dlong * cos lat = 1200 * cos 45° = 848.5′
For 60° N:
dep = dlong * cos lat = 1200 * cos 60° = 600′
A ship in position 41° 10′ S 032° 45′ W is steaming a course of 090° T at a speed of 16 knots. Find the longitude reached after 22 hours of steaming.
Distance covered in 22 hours = 22 * 16 = 352′
In parallel sailing, dep = distance = 352′
dep = dlong * cos lat
dlong = dep / cos lat = 352 / cos 41° 10′ = 7° 47.6′ E (Direction E because course is 090° T)
Initial longitude – 032° 45′ W , dlong – 7° 47.6′ E
So, Final longitude = 024° 57.4′ W
Plane Sailing
In plane sailing, dlat – dep – dist – course are considered to form the plane of a right angled triangle.
Plane sailing formula should not be calculated for distance more than 600′.
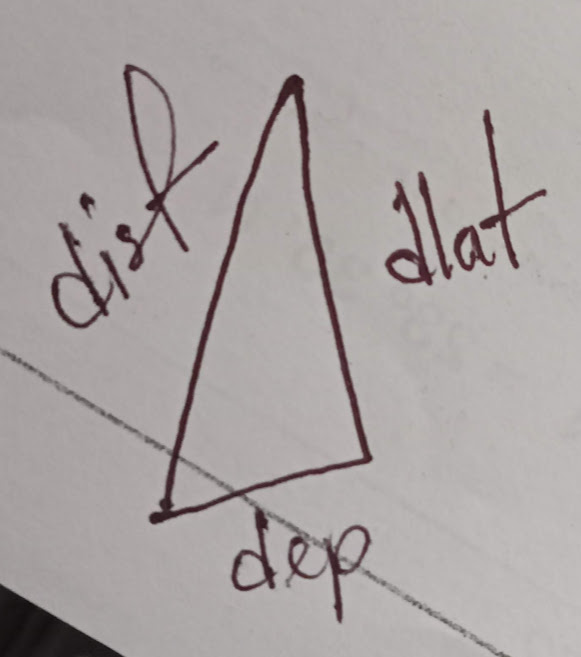
In plane sailing formula:
- sinco = dep / dist
- cosco = dlat / dist
- tanco = dep / dlat
- dep = dlong * cos m’lat
- mean lat = (N + N)/2 or, (N – S)/2
- dlat same name (-) and opposite name (+); direction towards to destination
- Final lat = Initial lat – dlat (if name opposite)
- Final lat = Initial lat + dlat (if name same)
Find the distance travelled and course steered by a ship that has moved 45′ to the south and 30′ to the west of its initial position.
Here, dlat = 45′ and dep = 30′
tanco = dep / dlat = 30 / 45 = 33.7° = S 33.5° W
cosco = dlat / dist
So, dist = dlat / cosco = 45 / cos 33.7° = 54.1′
If a ship covers a distance of 35′ in a general north easterly direction and changes its latitude by 20°, find the course that it has steered.
Here, dlat = 20° and dist = 35′
We know, cosco = dlat / dist = 20 / 35 = 55.1° = N 55° E or 55° T
If a ship departs from position 24° 30′ N 038° 20′ W for 22° 40′ N 039° 35’W, find the course and distance travelled by the ship.
Direction – SW
dlat = 24° 30′ N – 22° 40′ N = 1° 50 ‘ S = 110’
dlong = 038° 20′ W – 039° 35′ W = 001° 15′ W = 75′
mean latitude = (24° 30′ + 22° 40′) / 2 = 23° 35′ N
dep = dlong * cos m’lat = 75 * cos 23° 35′ = 68.74′ W (direction as dlong)
tanco = dep / dlat = 68.74 / 110 = 32° = S 32° W = 212° T
cosco = dlat / dist;
So, dist = dlat / cosco = 110 / cos 32 = 129.7′
If a ship departs from position 34° 20′ S 040° 30′ W on a course of 033° T for 350′; find the position reached.
Here, Course = 033° T = N 33° E
dist = 350′
cosco = dlat / dist
So, dlat = cosco * dist = cos 33° * 350′ = 04° 53.5′ N
Final lat = Initial lat – dlat = 34° 20′ S – 04° 53.5′ N = 29° 26.5′ S
mean lat = (34° 20′ S + 29° 26.5′ S) / 2 = 31° 53.25′ S
sinco = dep / dist
So, dep = sinco * dist = sin 33° * 350 = 190.6′
dep = dlong * cos m’lat
So, dlong = dep / cos m’lat = 190.6 / cos 31° 53.25′ = 3° 44.5′ E
Final longitude = 040° 30′ W- 3° 44.5′ E = 036° 45.5′ W
Position reached = 29° 26.5′ S 036° 45.5′ W
Mercator Sailing
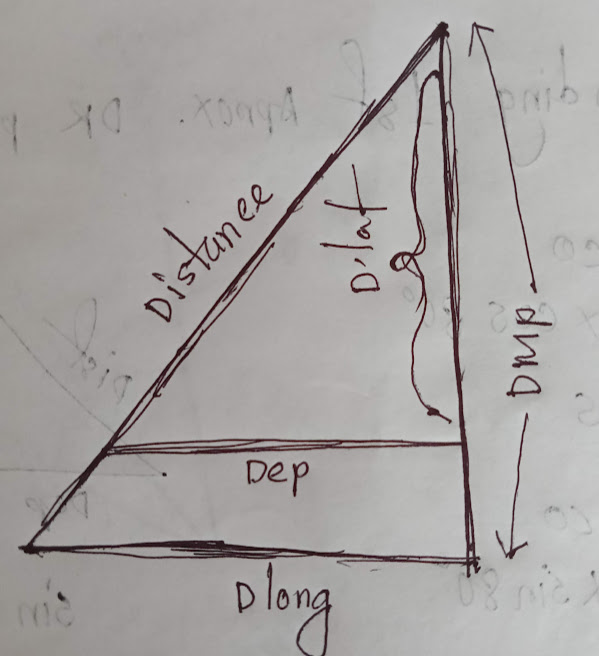
- Mercator sailing uses DMP and dlong instead of dlat and dep.
- DMP = Difference of meridional parts
- MP value can be found in nautical tables.
- IF same latitude, DMP = MP1 – MP2 (same names subtract AND different names add)
- dlat = DMP
- dlong = departure
- Mercator sailing provides greater accuracy
- In Mercator projection, meridians appear @ right-angles to the earth’s equator, and lines of latitude are horizontal lines whose actual distance increases from the equator towards the pole.
Determine the Mercator course and distance between 20° 24′ S 057° 26′ E and 34° 10′ S 112° 28′ E.
Direction – SE
dlat = 20° 24′ S – 34° 10′ S = 13° 46′ = 826′ S
dlong = 057° 26′ – 112° 28′ = 055° 02′ = 3302′ E
We have got MP, 1242.56 and 2170.41
So, DMP = 1242.56 – 2170.41 = 927.85
tanco = dlong / DMP = 3302 / 927.85 = 74.3° = S 74.5° E = 105.5° T
cosco = dlat / dist
So, dist = dlat / cosco = 826 / cos 74.3° = 3053′
If a ship departs from position 46° 14′ N 125° 36′ W on a course of 237° T and covers 7076′, find the position reached.
Course = 237° T = S 57° W
dlat = distance x cos course = 7076′ x cos 57° = 64° 13′.9 S
Arrived lat = 46° 14′ N – 64° 13′.9 S = 17° 59.9′ S
46° 14′ N – MP 3118.83
17° 59.9′ S – MP 1090.885
So, DMP 4209.715
d.long = tan course x DMP = tan 57° x 4209.715 = 108° 02.4′ W
Arrived long = departure long + d.long = 125° 36.0′ W + 108° 02.4′ W = 126° 21.6′ E (Subtraction of 360° has been carried out)
Position reached = 17° 59.9′ S 126° 21.6′ E
