Angle of Heel or List (Derrett Stability)

by

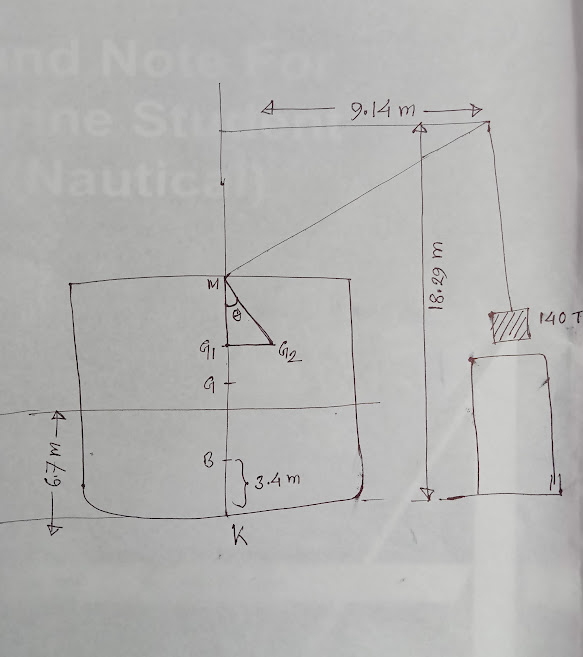
Angle of Heel or List (Derrett Stability)

A ship is just about to lift a weight from a jetty and place it on board. Using the data given below, calculate the angle of the heel after the weight has just been lifted from this jetty. The weight to be lifted is 140 t with an outreach of 9.14 m. The displacement of the ship before the lift is 10060 tonnes. Before liftoff, the KB is 3.4 m. KG is 3.66 m, TPCsw is 20, INA is 22788 m4, and the draft is 6.7 m in salt water. The height to derrick’s head is 18.29 m above the keel.

Angle of Heel or List

Angle of Heel or List (Derrett Stability)

Mass = Vol * Density

V = M / d = 10060 / 1.025 = 9814.63 m3

I = 22788 m4

BM = I / V = 22788 / 9814.63 = 2.32 m

KM = KB + BM = 3.4 + 2.32 = 5.72 m

G1G2 = (w * d) / W = (140 * 9.14) / 10200 = 0.125 m ; because 10060 + 140 = 10200 MT

Moment about the keel:

Initial weight 10060 * KG 3.66 = Moment 36819.6

weight 140 * KG 18.29 = Moment 2560.6

Total weight = 10200 and Final moment = 39380.2

Final KG (KG1) = Final moment / Final displacement = 39380.2 / 10200 = 3.86 m

KG1 = 3.86 m

G1M = KM – KG1 = 5.72 – 3.86 = 1.86 m

G1M = 1.86 m

In the triangle G1G2M (drawing), tan@ = G1G2 / G1M = 0.125 / 1.86 ;;; So, @ = 3° 50.7′

Angle of Heel or List (Derrett Stability)

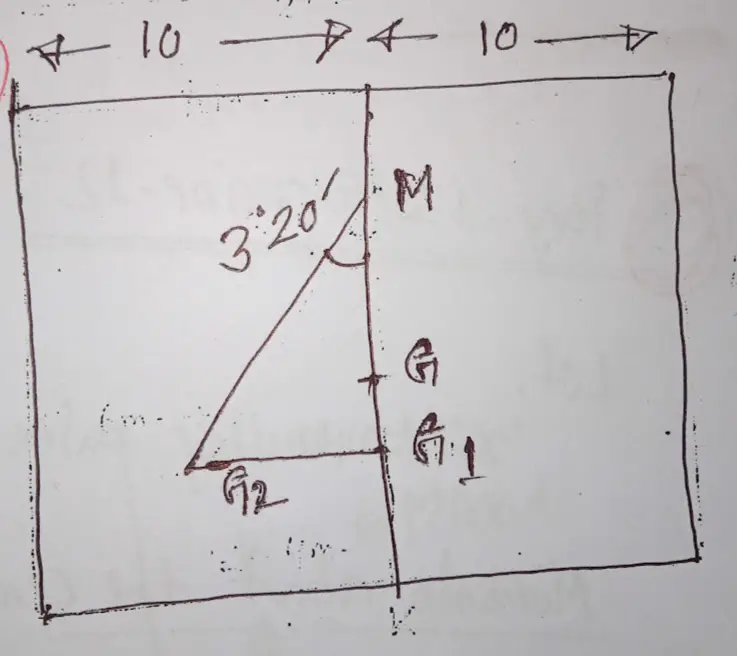
A ship of 7500 tonnes displacement has KM 8.6 m, KG 7.8 m, and 20 m beam. A quantity of deck cargo is lost from the starboard side (KG 12 m, and center of gravity 6 m in from the rail). If the resulting list is 3 degrees 20 minutes to port, find how much deck cargo was lost.

deck cargo was lost 91 tonne

Let x tonnes of deck cargo was lost

d = 12 – 7.8 = 4.2 m

GG1 = w * d / W – w = (x * 4.2) / (7500 – x)

= 4.2x / 7500 – x

G1G2 = w * d / W -w = x * 4 / 7500 – x (20/2 = 10 – 6 = 4)

= 4x / 7500 – x

KM = 8.6 m

KG = 7.8 m

GM = 0.8 m

G1M = GM + GG1 = 0.8 + (4.2x / (7500 – x)) = (6000 + 3.4x) / 7500 – x

In triangle, G1G2M, Tan@ = G1G2 / G1M

Tan 3° 20′ = (4x / (7500 – x)) / (6000 + 3.4x) / 7500 – x

x = 91.5 tonne (Ans.)

(Derrett Stability)

A ship of 7800 tonnes displacement has a mean draft of 6.8 m and is to be loaded to a mean draft of 7 meters. GM = 0.7 m and TPC = 20 tonnes. The ship is at present listed 4 degrees to starboard. How much more cargo can be shipped in the port and starboard tween deck, centers of gravity 6 m and 5 m, respectively, from the centreline, for the ship to complete loading and finish upright?

183 tonne of cargo to load

Final draft = 7.0 m

Initial draft = 6.8 m

Increase in draft = 0.2 m = 20 cm

Cargo to load = increase in draft * TPC = 20 * 20 = 400 tonnes

Let x tonne cargo to load in port side twin deck and (400 – x) tonne cargo to load in starboard side twin deck.

In triangle GG1M, Tan@ = GG1 / GM

GG1 = GM * Tan@ = 0.7 * Tan 4° = 0.049 m

Weight 7800 * distance 0.049 = Listing Moment to stbd 382.2

Weight (400 -x) * distance 5 = Listing moment to stbd 2000 – 5x

Weight x * distance 6 = Listing moment to port 6x

If the ship is to bring upright then, Listing moment to port = Listing moment to stbd

6x = 382.2 + 2000 – 5x

6x + 5x = 2382.2

11x = 2382.2

x = 216.56 tonnes cargo to load in port side

So, cargo to load starboard side = 400- 216.56 = 183.44 tonnes (Ans.)